4.3. 確率計算の統合

規格Part 10ではSMの診断率DCを$K_\text{IF,RF}$、SM2の診断率DC2を$K_\text{SM,MPF}$としています。それらを用いれば(988.1)は、 $$ \Pr\{\text{VSG}\}=\Pr\{\text{VSG.RF}\}+\Pr\{\text{VSG.DPF'}\}\\ =\Pr\{\overline{\text{IF}}\cap\overline{\text{DC}}\}+\frac{1}{2}\Pr\{\overline{\text{IF}}\}\Pr\{\overline{\text{SM}}\cap\text{DC}\}\\ =(1-\text{DC})\Pr\{\overline{\text{IF}}\}+\frac{1}{2}\text{DC}\Pr\{\overline{\text{IF}}\}\Pr\{\overline{\text{SM}}\}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}T_\text{lifetime}+\frac{1}{2}K_\text{IF,RF}\lambda_\text{IF}T_\text{lifetime}\left[(1-K_\text{SM,MPF})\lambda_\text{SM}T_\text{lifetime}+K_\text{SM,MPF}\lambda_\text{SM}\tau\right]\\ =(1-K_\text{IF,RF})\lambda_\text{IF}T_\text{lifetime}+\frac{1}{2}K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}\left[(1-K_\text{SM,MPF})T_\text{lifetime}+K_\text{SM,MPF}\tau\right]\tag{990.1}\label{eq:1} $$ よって、PMHFは\eqref{eq:1}の両辺を$T_\text{lifetime}$で割って求められるので、 $$ M_\text{PMHF}=\frac{1}{T_\text{lifetime}}\Pr\{\text{VSG}\}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+\frac{1}{2}K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{SM,MPF})T_\text{lifetime}+K_\text{SM,MPF}\tau\right]\tag{990.2}\label{eq:2} $$

4.4 規格式との比較

これは規格第1版のPMHF式と正確に一致します。規格式は両辺を$T_\text{lifetime}$で割ることをわざわざ明示しています。

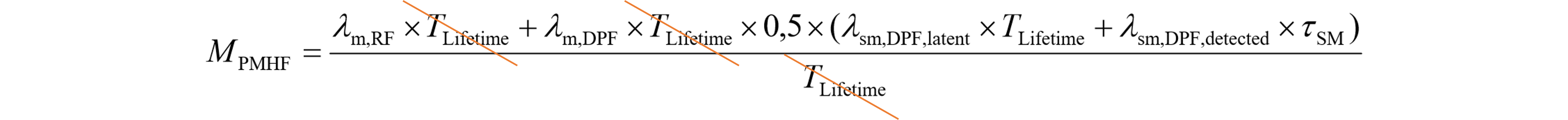
ただし、以下のように読み替えます。$\text{m}\rightarrow\text{IF}$、$\text{sm}\rightarrow\text{SM}$、他の定数はPart 10で定義されています。 $$ \begin{eqnarray} \begin{cases} \lambda_\text{m,RF}&=(1-K_\text{IF,RF})\lambda_\text{IF}\\ \lambda_\text{m,DPF}&=K_\text{IF,RF}\lambda_\text{IF}\\ \lambda_\text{sm,DPF,latent}&=(1-K_\text{SM,MPF})\lambda_\text{SM}\\ \lambda_\text{sm,DPF,detected}&=K_\text{SM,MPF}\lambda_\text{SM}\\ \end{cases} \end{eqnarray}\tag{990.3}\label{eq:3} $$ 図104.2で示すように規格初版のPMHF式には0.5という定数がありましたが、実は「SMが先に故障した場合に限る」ことから0.5が掛かっていたわけでした。

前のブログ 次のブログ