「ISO 26262第2版解説書」(日本規格協会)のPMHF式と別の方法ですが、弊社の方法で計算し直します。弊社のやり方はCTMCの原理を用い、時刻$t$におけるDPF確率密度を求め、$0$から$T_\text{lifetime}$まで積分するというものです。

パターン1

• Pattern 1: SM1⇒IFの順にフォールトが発生し、SM1のフォールトはSM2によって緩和されるが通知されない、または緩和されない。フォールトの暴露時間は、最悪の場合の暴露時間である車両寿命となる。

パターン1は、SM1のフォールトが2nd SM(SM2)で検出されないため、SM1のフォールト全体に対するパターン1の割合は$1-K_\text{SM,DPF}$となり、マルコフ図は以下のようになります。時刻パラメータ$t$までに最初のSMのフォールトが起き、$t'(\approx t)$がVSGとなる2つ目のIFのフォールトが起きた時刻とします。

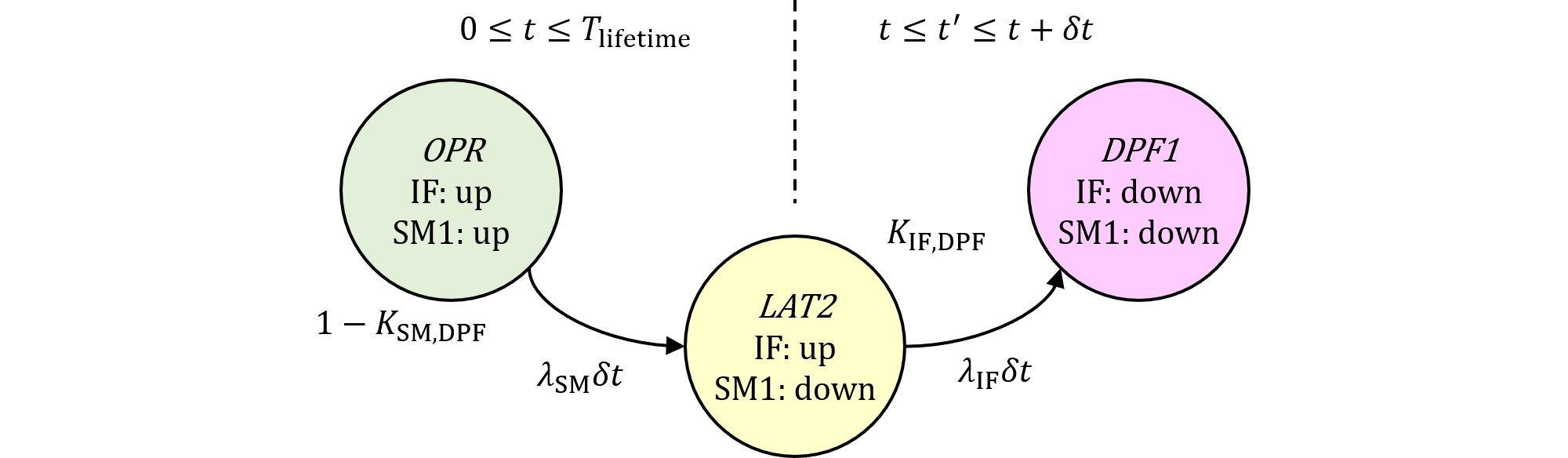
PMHFの求め方は、IFのフォールトに関する$t$から$t+\delta t$までのDPF確率密度を求めます。次にサブシステムについて、DPF VSGとなる確率密度を0から$T_\text{lifetime}$まで積分します。

まず、検出されない部分のSM1の$LAT2$での状態確率は、 $$\begin{eqnarray} \Pr\{\text{SM1(undet) in }LAT2\}&=&\Pr\{\text{SM1 down at }t\cap\text{SM1 fault not detected}\}\\ &=&(1-K_\text{SM,DPF})F_\text{SM}(t) \end{eqnarray}\tag{474.1}$$ 次にIFの$LAT2$での状態確率は、 $$\begin{eqnarray} \Pr\{\text{IF in }LAT2\}&=&\Pr\{\text{IF up at }t\cap\text{IF fault prevented}\}\\ &=&\Pr\{\text{IF up at }t\}\Pr\{\text{IF fault prevented}\} &=&K_\text{IF,DPF}R_\text{IF}(t) \end{eqnarray}\tag{474.2}$$

$LAT2$から$DPF1$への微小時間間隔$\delta t$での遷移確率は、IFがフォールトによりDPFとなる場合であり、

$$d\!\Pr\{\text{IF down in }(t, t+\delta t] | \text{IF up at }t\}=\lambda_\text{IF}\delta t \tag{474.3}$$

従って、状態確率(474.2)と遷移確率(474.3)の積をとりIFの$(t, t+\delta t]$における確率密度を求めれば、 $$\begin{eqnarray} d\!\Pr\{\text{IF in }LAT2&\text{ at }&t\cap\text{IF down in }(t, t+\delta t]\}\\ &=&d\!\Pr\{\text{IF up at }t\cap\text{IF fault prevented}\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\Pr\{\text{IF up at }t\}\Pr\{\text{IF fault prevented}\}\\ &&\cdot d\!\Pr\{\text{IF down in }(t, t+\delta t] | \text{IF up at }t\}\\ &=&K_\text{IF,DPF}R_\text{IF}(t)\lambda_\text{IF}\delta t=K_\text{IF,DPF}f_\text{IF}(t)\delta t \end{eqnarray}\tag{474.4}$$

IFとSM1にはフォールトの生起について独立であるため、各々の確率はかけることができます。よって、 IFの項(474.4)とSM1の項(474.1)の積をとり、$0$から$T_\text{lifetime}$まで積分して時間平均をとると、 $$\begin{eqnarray} M_\text{PMHF,fsm,P1}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{LAT2 at }t\cap\text{IF fault prevented}\\ &&\cap\ \text{IF down in }(t, t+\delta t]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{IF up at }t\cap\text{SM1 down at }t\\ &&\cap\ \text{SM1 fault not detected}\cap\ \text{IF fault prevented}\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\text{SM1 down in }[0, t)\cap\text{SM1 fault not detected}\}\\ &&\cdot d\!\Pr\{\text{IF down in }[t, t+\delta t)\cap\text{IF up at }t\cap\text{IF fault prevented}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_\text{SM,DPF})F_\text{SM}(t)K_\text{IF,DPF}f_\text{IF}(t)dt\\ &\approx&\frac{1}{2}K_\text{IF,DPF}(1-K_\text{SM,DPF})\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}\\ &=&\frac{1}{2}\lambda_\text{SM,DPF,lat}\lambda_\text{IF,DPF}T_\text{lifetime} \end{eqnarray}\tag{474.5}$$ なお、式変形中に弊社積分公式を使用しています。

(474.5)は図474.2に引用する規格第2版式のPattern 1と正確に一致します。

さらに(474.5)は、図474.3に引用する規格初版第1式のパターン1に相当する部分(図の黄色部分)とも(IF⇒mと読み替えることにより)正確に一致します。

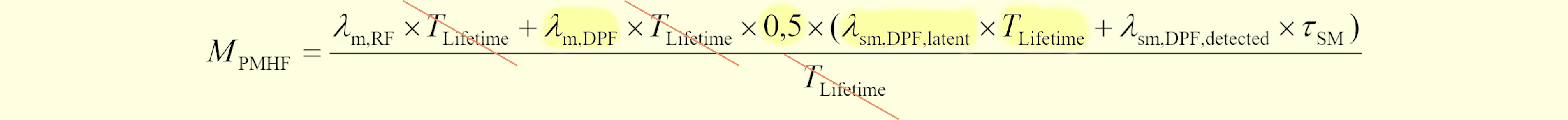
このようにCTMCを用いて、時刻$t$におけるDPF確率密度を0から車両寿命まで積分する方法のほうが、ずっと簡単でわかりやすいです。

なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

前のブログ 次のブログ