「ISO 26262第2版解説書」(日本規格協会)のPMHF式の解読を行います。この記事の続きです。

パターン1

パターン1を規格に従って計算します。

• Pattern 1: SM1⇒IFの順にフォールトが発生し、SM1のフォールトはSM2によって緩和されるが通知されない、または緩和されない。フォールトの暴露時間は、最悪の場合の暴露時間である車両寿命となる。

規格にはマルコフ図が記載されていないので推測すると、パターン1は、SM1のフォールトが2nd SM(SM2)で検出されないため、SM1のフォールト全体に対するパターン1の割合は$1-K_\text{SM,DPF}$となり、マルコフ図は以下のようになります。時刻パラメータ$t$が最初のSMのフォールトが起きた時刻、$t'$がVSGとなる2つ目のIFのフォールトが起きた時刻とします。

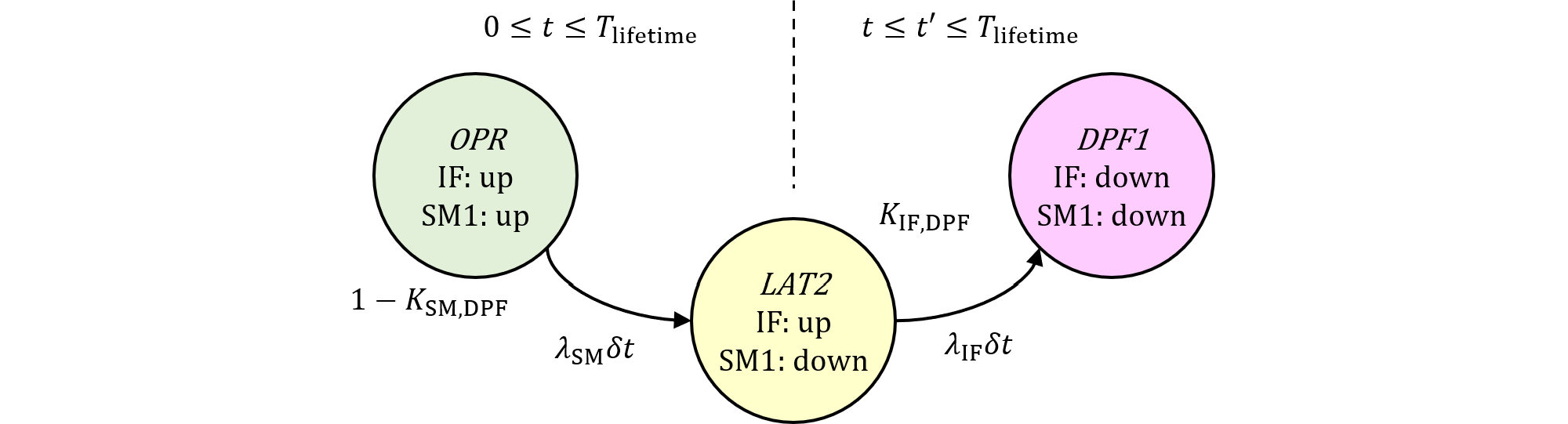
規格によるPMHFの求め方は、
1. 後に起きるIFのフォールトの確率密度を$t$から$T_\text{lifetime}$まで$t'$について積分し$t$で表します。$t'$まではIFはフォールトしないことに注意します。
2, 先に起きるSMのフォールトの確率密度を0から$T_\text{lifetime}$まで$t$について積分します。

まず、IFの$LAT2S$での状態確率は、 $$\Pr\{\text{IF in }LAT2S\}=\Pr\{\text{IF up at }t'\cap\text{VSG of IF prevented}\}=K_\text{IF,DPF}R_\text{IF}(t') \tag{471.1}$$ $LAT2S$から$DPF1$への微小時間での遷移確率は、IFがDPFする場合であり、 $$\Pr\{\text{IF down in }(t', t'+dt']\ |\ \text{IF in }LAT2S\}\\ =\Pr\{\text{IF down in }(t', t'+dt']\ |\ \text{IF up at }t'\cap\text{VSG of IF prevented}\}\\ =\Pr\{\text{IF down in }(t', t'+dt']\ |\ \text{IF up at }t'\}=\lambda_\text{IF}dt' \tag{471.2}$$

規格のとおりIFの確率を求めるには、IFは時刻$0$から$t'$まではフォールトせず(解説書の$t$は誤り)、かつ、$t'$から$T_\text{lifetime}$までにフォールトする確率となります。

従って、(471.1)、(471.2)から、IFの後故障の確率を求めると $$K_\text{IF,DPF}\int_t^{T_\text{lifetime}}R_\text{IF}(t')\lambda_\text{IF}dt'=K_\text{IF,DPF}\int_t^{T_\text{lifetime}}f_\text{IF}(t')dt'\\ =K_\text{IF,DPF}\left[F_\text{IF}(t')\right]^{T_\text{lifetime}}_t=K_\text{IF,DPF}\left[F_\text{IF}(T_\text{lifetime})-F_\text{IF}(t)\right]\\ \approx K_\text{IF,DPF}\lambda_\text{IF}(T_\text{lifetime}-t) \tag{471.3}$$ ところが、解説書パターン1では以下のようになっており、2か所の誤りが存在します。

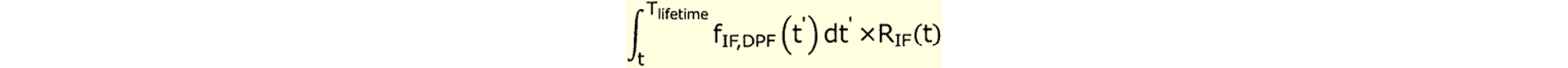
次にSMの$OPRS$での状態確率は、 $$\Pr\{\text{SM in }OPRS\}=\Pr\{\text{SM is up at }t\}=R_\text{SM}(t) \tag{471.4}$$ $OPRS$から$LAT2S$への微小時間での遷移確率は、SMがフォールトする場合であり、 $$\Pr\{\text{SM down in }(t, t+dt] | \text{SM is up at }t\}=(1-K_\text{SM,DPF})\lambda_\text{SM}dt \tag{471.5}$$

IFの項とSMの項を$0$から$T_\text{lifetime}$まで積分し時間平均すると、(471.3)～(471.5)を用いて、 $$\require{cancel} M_\text{PMHF,P1}\approx\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_\text{SM,DPF})R_\text{SM}(t)\lambda_\text{SM}K_\text{IF,DPF}\lambda_\text{IF}(T_\text{lifetime}-t)dt\\\ \approx\frac{1}{\bcancel{T_\text{lifetime}}}(1-K_\text{SM,DPF})K_\text{IF,DPF}\lambda_\text{IF}\lambda_\text{SM}\left[T_\text{lifetime}\bcancel{t}-\frac{1}{2}t^\bcancel{2}\right]_0^{T_\text{lifetime}}\\ =\frac{1}{2}K_\text{IF,DPF}(1-K_\text{SM,DPF})\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}\\ =\frac{1}{2}\lambda_\text{SM,DPF,lat}\lambda_\text{IF,DPF}T_\text{lifetime} \tag{471.6}$$

これは図104.2の初版PMHF式(パターン1, 2のみ)の、DPFにおけるパターン1に相当する部分と(IF⇒mと読み替えることにより)正確に一致します。

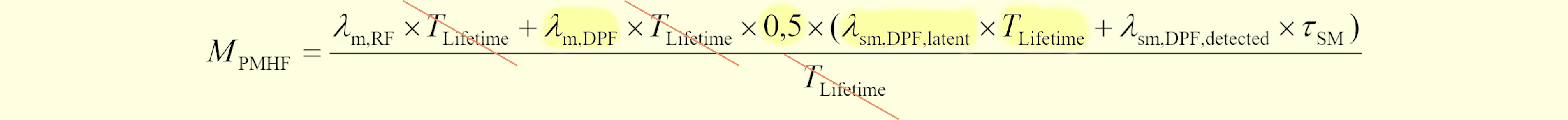
なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

ほぼ同様な議論ですが、記事#476に再掲します。

前のブログ 次のブログ