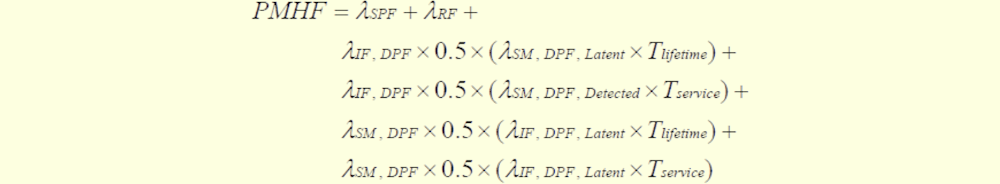LFMの導出
LFM、$M_{\mathrm{LFM}}$に関する規格式を引用し、これを導出します。
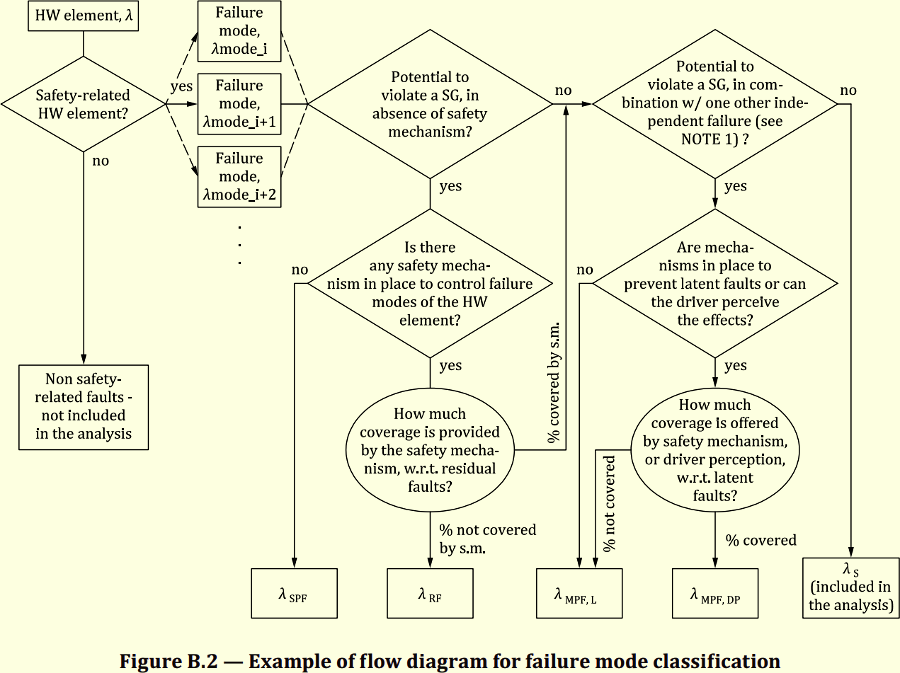
 図123.1 LFM規格式
図123.1 LFM規格式
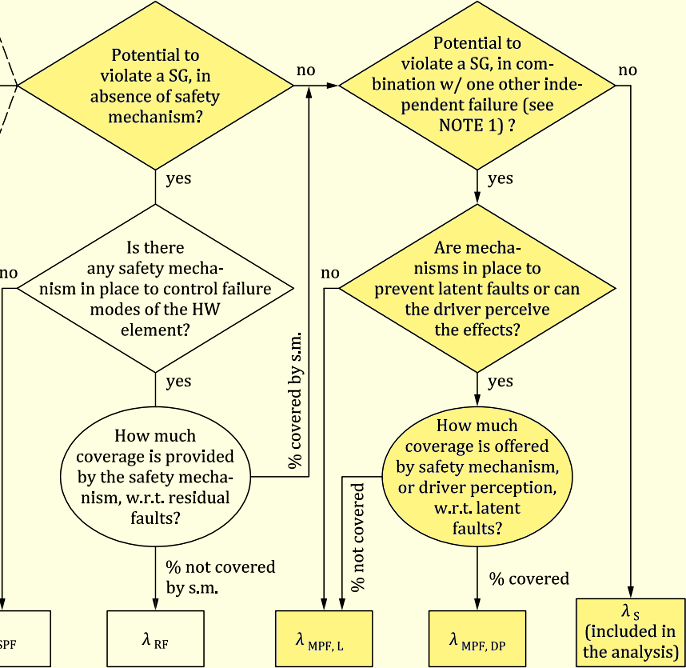
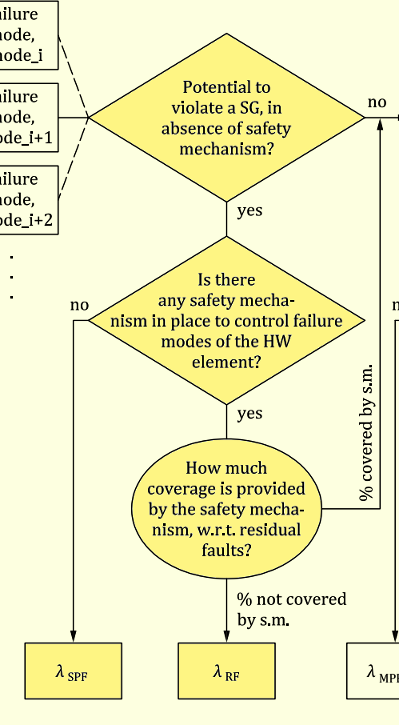
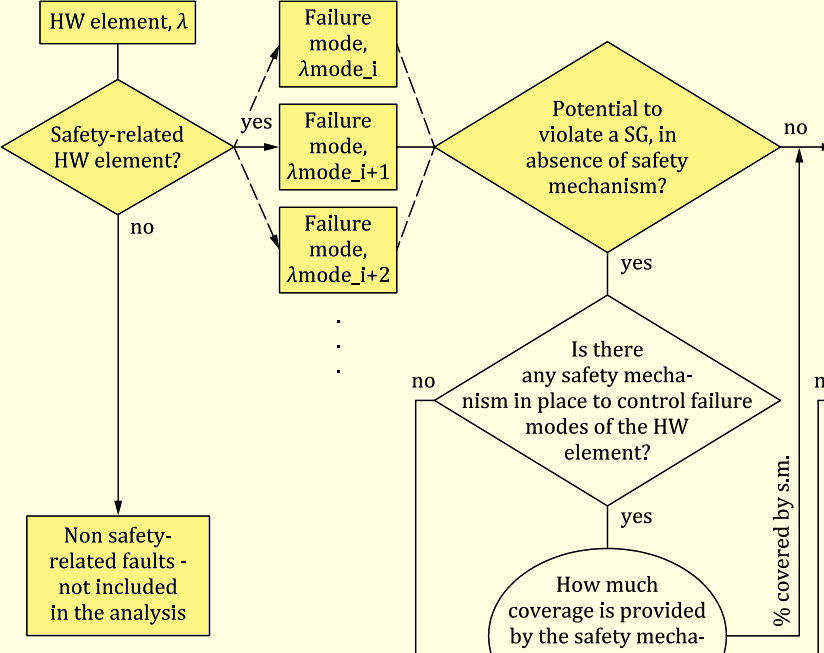
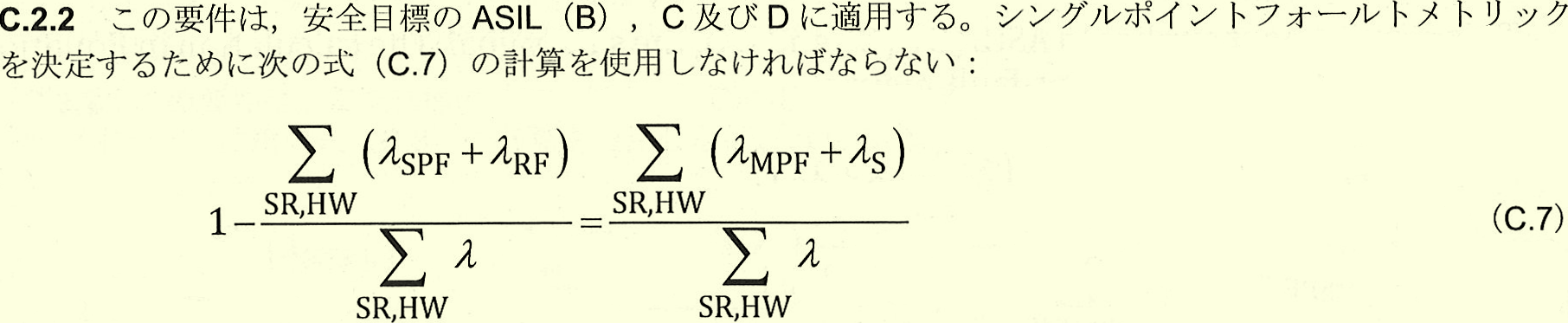
前稿と同様な論証を行います。まずレイテントフォールト(LF)の故障率の計算式を見てみます。
故障分類フローで説明したように、レイテントフォールトとなるのは2とおり存在します。
- 主機能のフォールトのSG侵害が1st SMにより抑止されている場合に、2nd SMで検出できない場合
- SMのフォールト(これはSG侵害が起こらない)が2nd SMで検出できない場合
よって、安全関連に関する故障モードが$n$個ある場合に、i番目のLFの故障率$\lambda_{\mathrm{LF,}i}$の定義式は、存在しない$\lambda_i$に対しては0を返すものとすれば、
$$
\lambda_{\mathrm{LF,}i}:=DC_i\lambda_{\mathrm{IF,}i}(1-DC2_i)+\lambda_{\mathrm{SM,}i}(1-DC2_i)=\{DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i}\}(1-DC2_i), \\
i=1, 2, ..., n\tag{123.1}
$$
と表せます。この$DC2_i$はKパラメータで書けば、
$$
DC2_i=K_{\mathrm{IF,FMC,MPF,}i}, もしくは K_{\mathrm{SM,FMC,MPF,}i}
$$
で、2nd SMがIFもしくはSMに対して、故障検出する割合を表します。(123.1)の両辺の総和を取れば、
$$
\sum_{i=1}^n\lambda_{\mathrm{LF,}i}=\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})(1-DC2_i)\\
=\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})-\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i
\tag{123.2}
$$
よって、$\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})$及び$\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i$を移項し、
$$
\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i=\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})-\sum_{i=1}^n\lambda_{\mathrm{LF,}i}
\tag{123.3}
$$
ここで、DC2の、各々の故障率による加重平均を(123.4)のように定義し、(123.3)を(123.4)の分子に代入すれば、
$$
\overline{DC2}:=\frac{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i}{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})}
=\frac{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})-\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})}\\
=1-\frac{\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})}
\tag{123.4}
$$
ここで、$DC_i\lambda_{\mathrm{IF,}i}=\lambda_{\mathrm{IF,}i}-\lambda_{\mathrm{RF,}i}$を代入すれば、(123.4)は
$$
(123.4)=1-\frac{\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(\lambda_{\mathrm{IF,}i}-\lambda_{\mathrm{RF,}i}+\lambda_{\mathrm{SM,}i})}=1-\frac{\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(\lambda_i-\lambda_{\mathrm{RF,}i})}\tag{123.5}
$$
これと(C.8)を比較すれば、$\img[-1.35em]{/images/withinseminar.png}$
 前のブログ
次のブログ
前のブログ
次のブログ