|
7 |
確率コントリビューション (6) |
 |
ストレートフォワード
そもそもIFとSM1のコンビネーションの確率全体を求め、以下の
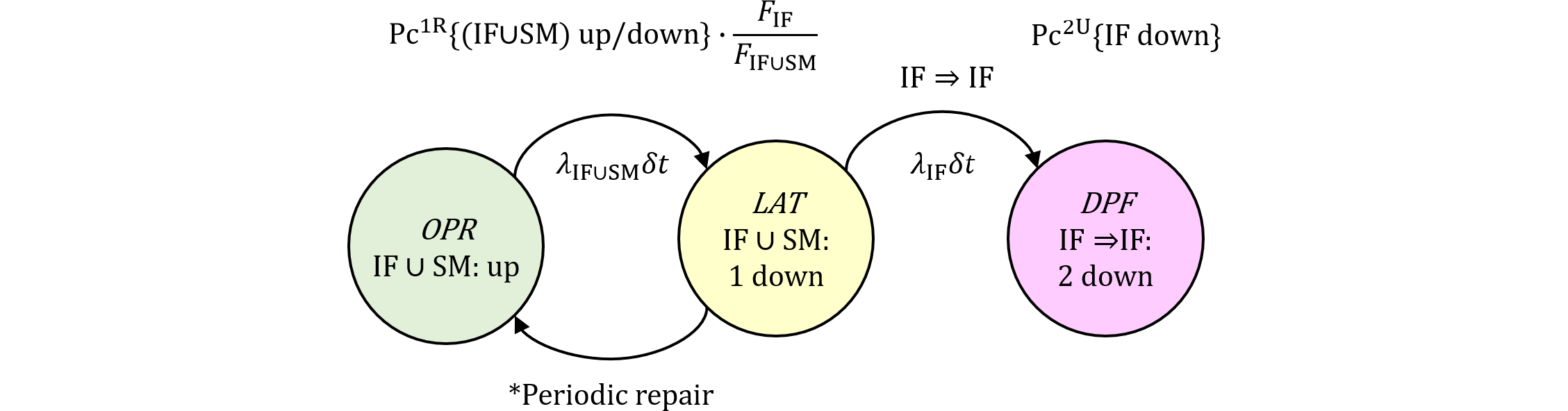
①IF⇒IF
②IF⇒SM1
③SM1⇒IF
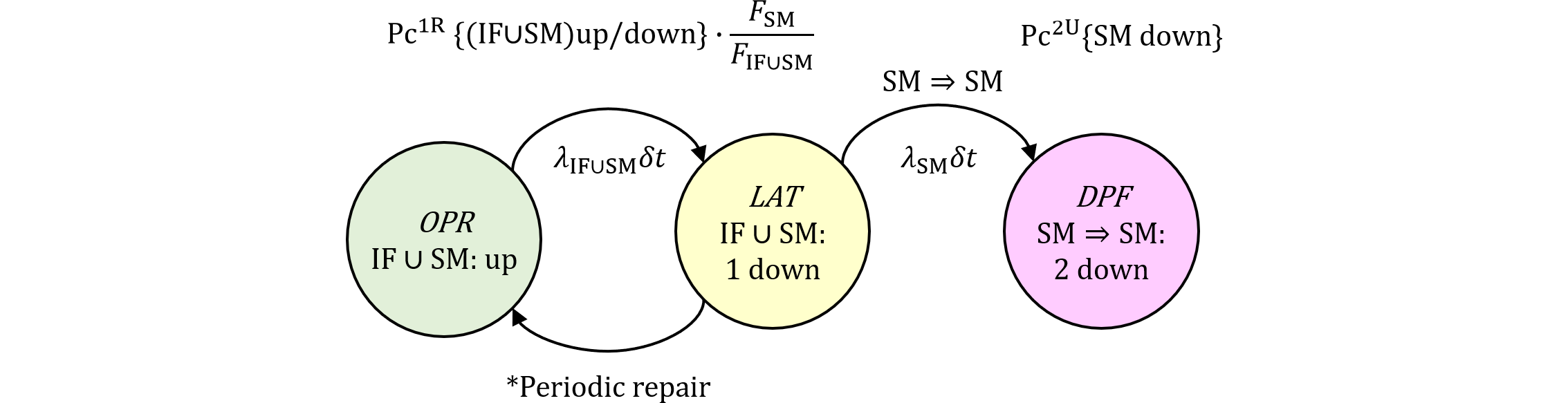
④SM1⇒SM1
①~④の和から①と④を引いたのですが、各々を求められるのであれば、DPFの対象は異なるエレメントのフォールトの組み合わせなので、②と③の和で良いはずです。
従って、②のPMHFは記事#489を参照して、 $$ M_\text{PMHF,DPF,IF⇒SM1} =\text{Pc}^\text{1R}\{\mathrm{(IF\cup SM)\ up/down}\} \cdot\frac{Q_\text{IF}(t)}{Q_{\text{IF}\cup\text{SM}}(t)}\cdot\text{Pc}^\text{2U}\{\text{SM down}\}\\ \approx\frac{K_\text{IF,RF}}{2}\lambda_\text{IF}\lambda_\text{SM}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \tag{491.1} $$
また③のPMHFも同様に $$ M_\text{PMHF,DPF,SM1⇒IF} \approx\frac{K_\text{IF,RF}}{2}\lambda_\text{IF}\lambda_\text{SM}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \tag{491.2} $$ 従って、PMHFのDPF部分は、(491.1)及び(491.2)を加えて $$ \require{cancel} \begin{eqnarray} M_\text{PMHF,DPF}&=&M_\text{PMHF,DPF,IF⇒SM1}+M_\text{PMHF,DPF,SM1⇒IF}\\ &=&(\bcancel{2}\lambda_\text{IF}\lambda_\text{SM})\frac{K_\text{IF,RF}}{\bcancel{2}}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau]\\ &=&K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \end{eqnarray} \tag{491.3} $$ これは過去記事で求めた、(222.9)のPMHF値のDPF項と完全に一致します。
さらに、2021年論文のようにLFMと互換性のあるPMHFを考えるのであれば、IFのMPFフォールトはレイテントにならずに直ちに修理されると考えると、DPFのケースは③のみとなります。従って、PMHFは $$ \begin{eqnarray} M_\text{PMHF,DPF} &\approx&\frac{K_\text{IF,RF}}{2}\lambda_\text{IF}\lambda_\text{SM}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \end{eqnarray} \tag{491.4} $$
となります。ただし、非冗長系においてはIFのフォールトは即時修理され、レイテントとならないことから$K_\text{IF,MPF}=0$となるので、これを代入すれば、$K_\text{MPF}=K_\text{SM,MPF}$となり、(491.4)は、
$$ \begin{eqnarray} M_\text{PMHF,DPF} &\approx&\frac{K_\text{IF,RF}}{2}\lambda_\text{IF}\lambda_\text{SM}[(1-K_\mathrm{SM,DPF})T_\text{lifetime}+K_\mathrm{SM,DPF}\tau] \end{eqnarray} \tag{491.5} $$ となります。
なお、本稿はRAMS 2023に投稿中のため一部を秘匿していますが、論文公開後の2023年2月頃に開示予定です。RAMS 2023が終了したため、秘匿部分を開示します。
確率コントリビューションの稿 完■