弊社CTMCベース

一方、弊社の方式ではフォールト生起順序と積分順序は同一です。

図480.1 弊社CTMCベース 図480.1に従い、時刻$t$までのSM1の積分を先に実行し、その後IFの積分を0から車両寿命まで実行すれば、 $$M_\text{PMHF,fsm,P1}=\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF}) \int_0^{T_\text{lifetime}}f_\text{IF}(t)\left[\int_0^{t}f_\text{SM1}(t')dt'\right]dt\\ =\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF}) \int_0^{T_\text{lifetime}}F_\text{SM1}(t)f_\text{IF}(t)dt\quad\quad\color{red}{※}\\ \approx\frac{1}{2}K_\text{IF,DPF}(1-K_\text{SM1,DPF})\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}\tag{480.1}$$ となり、前稿と同じ値になります。導出には公式(60.6)を使用しました。

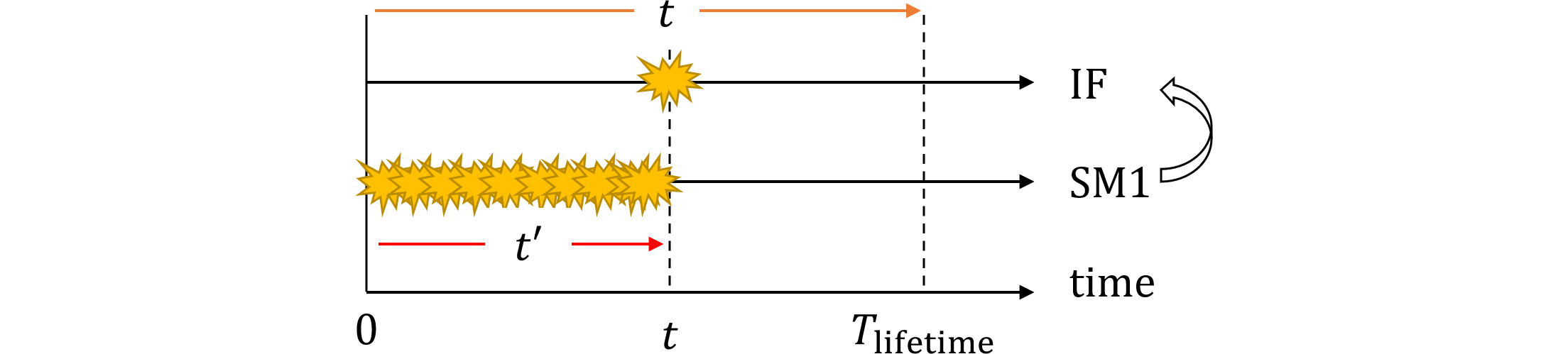
CTMC理論

CTMC理論に基づけば、時刻$t$におけるサブシステムのレイテントとなる状態確率は「SM1がdownかつSM2により非検出かつIFがup」であるため、 $$\Pr\{\text{SM1 down at }t\cap\text{fault not detected}\cap\text{IF up at }t\}=F_\text{SM1,DPF,lat}(t)R_\text{IF}(t)\\ =(1-K_\text{SM1,DPF})F_\text{SM1}(t)R_\text{IF}(t)\tag{480.2}$$ レイテント状態における微小時間間隔$dt$間の遷移確率(条件付き確率)は、公式(66.8)より $$\require{cancel} \Pr\{\text{IF down in }[t, t+dt)|\bcancel{\text{SM1 down at }t}\cap\text{IF up at }t\}=K_\text{IF,DPF}\lambda_\text{IF}dt\tag{480.3}$$ となります。従って確率は(480.2)と(480.3)の積を$0$から$T_\text{lifetime}$まで積分した $$K_\text{IF,DPF}(1-K_\text{SM1,DPF})\int_0^{T_\text{lifetime}}F_\text{SM1}(t)R_\text{IF}(t)\cdot\lambda_\text{IF}dt\tag{480.4}$$ となり、(480.1)$\color{red}{※}$で示すパターン1のDPF確率と一致します。

両者の比較

前稿の解説書の方式はフォールトと順序積分順序が逆ではあるものの、図479.1と図480.1を比較すれば、特に大きな問題はなさそうですし実際に結果も一致します。しかしながら、弊社の方式はCTMC理論でも裏付けされており、フォールトと順序積分順序も一致しているため、straight forwardだと考えます。

結論

本来の条件であるIFとSM1の両方がrepairableであるというシンプルな条件と異なるため、誤りではあるものの、規格第2版の前提と想定される、以下のおかしな条件(図313.1)によるPMHF式の導出はこれで完了です。

• サブシステムはIFとSM1とSM2から構成される。
• もしSM1のフォールトが最初に起きた場合、SM1はrepairableとなりIFはunrepairableとなる。
  　　・SM1のフォールトのSM2により検出されない部分は修理されず、暴露時間は$T_\text{lifetime}$となり、 (Pattern 1)
  　　・SM1のフォールトのSM2により検出される部分は修理され、暴露時間は$T_\text{service}$となり、 (Pattern 2)
  暴露時間中における引き続くIFの最初のフォールトでDPFが発生する。⇒IFUモデル
• もしIFのフォールトが最初に起きた場合、IFはrepairableとなりSM1はunrepairableとなる。
  　　・IFのフォールトのSM1により抑止されない部分は修理されず、暴露時間は$T_\text{lifetime}$となり、 (Pattern 3)
  　　・IFのフォールトのSM1により抑止される部分は修理され、暴露時間は$T_\text{service}$となり、 (Pattern 4)
  暴露時間中における引き続くSM1の最初のフォールトでDPFが発生する。⇒SMUモデル

なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

---

前のブログ 次のブログ